GME > G.스코어

G.스코어 G. Score

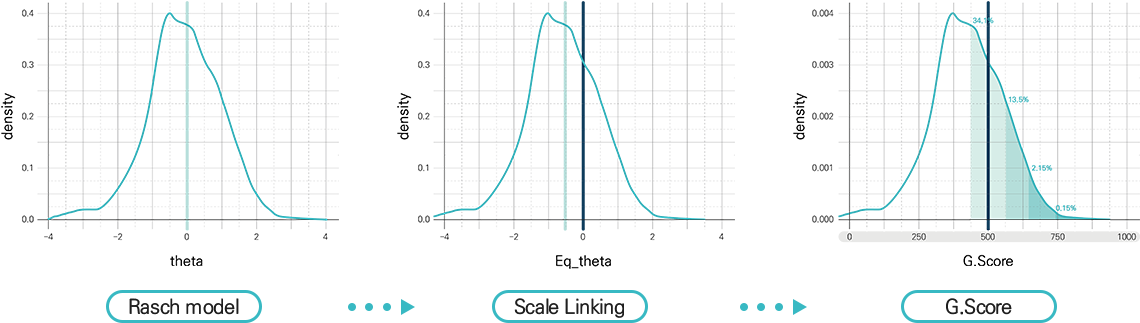
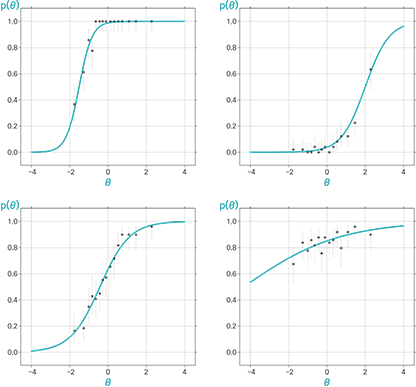
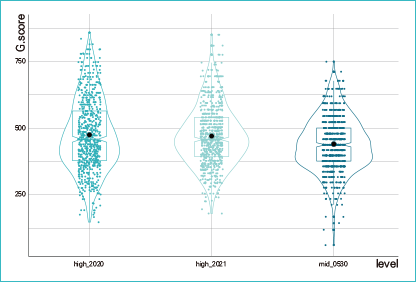
G.스코어는 TIMSS, PISA 등의 국제평가기구에서 활용되는 문항반응이론(Item Response Theory: IRT)과 척도 연계(Scale Linking) 방법을 이용하여 GME수학평가원에서 산출한 수학학습능력 지수입니다. IRT는 확률적 모형식을 이용하여 분석이 이루어지기 때문에 정답률을 이용하여 분석되는 고전검사이론에 비해 집단 특성의 영향을 적게 받는 장점이 있습니다. 특히 Rasch 모형은 IRT 모형 중에서 간결하고 적은 수의 표본에서도 적합한 분석이 이루어지는 모형으로 실제 평가 현장에서 주로 많이 사용되고 있습니다. Scale Linking은 동일 과목 내에서 다른 대상 및 다른 시기에 실시한 평가의 결과들을 같은 척도 상에 놓이게 함으로서 서로 간의 직접적인 비교가 가능하도록 해 주는 방법입니다. IRT와 Scale Linking 결과 산출된 GME수학평가원의 G.스코어를 통해 집단 내에서 개별 학생의 수학학습능력과 문항난이도의 상세한 비교 분석을 할 수 있습니다. 또한 아직 실시되지 않은 평가에 대해서도 학생별 결과를 예측할 수 있으며, 집단 간 비교에서는 수평적(동일학년), 수직적(상위학년) 수학학습능력 수준을 비교할 수 있습니다.

학생능력수준과 문항난이도
  • 학생능력수준

    학생능력수준은 각 문항의 응답 결과에 대해 Rasch 모형 적용을 위한 최대우도추정법을 통해 분석된 지수입니다. 학생능력수준의 지수값이 클 수록 우수한 학생을 나타내며, 같은 수의 문항을 맞힌 경우 쉬운 문항에서 어려운 문항을 순차적으로 맞힌 학생의 능력수준이 높게 추정됩니다. 학생능력수준은 문항난이도와 동일한 척도로 추정됩니다.

  • 문항난이도

    문항난이도는 문항이 어떤 학생의 능력수준에서 기능하는가를 나타내는 지수로서 문항난이도가 클수록 어려운 문항이고, 문항난이도가 작을수록 쉬운 문항임을 나타냅니다. 문항난이도는 학생능력수준과 동일한 척도로 추정됩니다.

Rasch 모형과 Scale Linking
  • Rasch모형

    Racsh모형은 문항의 각 난이도와 응답자의 반응을 결합하여 조사하고자 하는 잠재변수의 속성을 측정해 주는 도구로서, 단일 속성(unidimensionality)의 검증, 표본 독립성(sample invariance), 설문 독립성(item invariance, local independence)을 보장해 주는 방법입니다. 또한 Racsh모형은 문항의 적합도, 문항의 곤란도, 응답 범주(item category)의 적절성을 평가할 수 있습니다. 문항반응이론 중 1모수 모형인 Rasch 모형은 분석에 필요한 모수의 수가 적어 간결성과 안정성이 높아 현장에의 적용이 유리한 장점이 있습니다.

  • Scale Linking

    평가를 통해 측정된 점수들이 난이도 및 다른 통계적 특성들에 영향을 받지 않고 다른 평가와 상호 교환되어 사용될 수 있도록 하기 위해서는 그 점수들을 조정하는 통계적 과정의 Scale Linking(척도 연계) 과정이 필요합니다(Kolen & Brennan, 2004). 문항반응이론에 대한 척도 연계 방법 중에서 Rasch 모형을 이용한 분석 시에는 Mean-Mean 변환 방법이 가장 적합합니다. 그에 따라 G.스코어는 서로 다른 집단의 학생들의 능력수준과 문항난이도를 비교하기 위해 Rasch 모형과 Mean-Mean 동등화 방법을 이용하여 척도 연계를 하여 응시 대상과 응시 시기가 다른 평가들 간의 비교를 할 수 있습니다.

G.스코어의 활용
  • 선수과정 평가를 통한 학생 수준 예측

    현행과정과 선수과정 학습 집단의 수학학습능력 수준이 IRT와 Scale Linking을 통해 G.스코어로 변환되어 같은 척도 상에 놓이게 되어 서로 다른 집단 간의 수학학습능력 수준의 비교가 가능합니다. 즉, 중학생의 수학학습능력 수준이 각 고등학교에서의 수학 내신 등급에서 어느 정도에 위치하고 있는지 알 수 있습니다.

  • G.스코어를 통한 고교별, 등급별 수준 비교

    서로 다른 고등학교의 수학 내신 등급은 각 학교별 특징에 많은 영향을 받습니다. 따라서 일반적인 고전검사이론적 분석 방법으로는 고교별 내신 등급의 비교가 매우 어렵습니다. 그러나 다양한 고등학교 학생들의 평가결과들에 대해 IRT와 Scale Linking을 통해 산출한 G.스코어를 이용하여 각 고등학교의 내신 등급 수준을 비교할 수 있습니다.